Защо не е странно за 4 дни тотото да изтегли два пъти едни и същи числа
На 10 септември 2009 година Българската национална лотария разгласи, че печелившите цифри за тази седмица са 4, 15, 23, 24, 35 и 42. Съвсем необикновен набор от числа, бихте си помислили – единствено дето в тегленето 4 дни по-рано се пада безусловно същата композиция.
Разбира се, хората всеобщо желаят следствие, с цел да се разбере измамата – само че по този начин и не е открито никакво нарушаване. Което, правичката да си кажем, по нашите земи по никакъв начин не потушава съмненията…
Но в този случай би трябвало – тъй като се оказва, че странните съвпадения са доста по-вероятни, в сравнение с си мислите.
Идеята резултат с възможност 1: 40 000 000 да се появи 2 пъти в границите на 4 дни може да бъде малко умопомрачителна – по тази причина дано стартираме с по-прост образец. Колко огромна би трябвало да бъде една група от хора, с цел да има късмет двама от тях да имат общ рожден ден?
Може би ще се изненадате да научите, че отговорът е единствено 23.
Може би сте чували тази задача и преди – тя е много известна. Всъщност се споделя Парадокс на рождения ден, макар че в него няма нищо парадоксално – просто е ненадейно, че резултатът е толкоз малко число.
От математическа позиция обаче той си е напълно стабилен – даже и да не наподобява по този начин на пръв взор. „ Може би сте разсъждавали по следния метод: Има късмет единствено 1: 365, че някой различен човек ще има същия рожден ден като мен. Така че има възможност 364/365 души да имат друг рожден ден от моя “, изяснява статистикът Дейвид Ханд, почетен професор по математика и старши откривател в Имперския лицей в Лондон, в книгата си „ Принципът на невероятността: Защо съвпадения, чудеса и редки събития се случват всеки ден “ от 2014 година
„ Ако в стаята има n души, като всеки от останалите n – 1 има възможност 364/365 да има друг рожден ден от мен, то вероятността всички n – 1 да имат друг рожден ден от мен е 364/365 × 364/365 × 364/365 × 364/365 × 364/365 … × 364/365, като 364/365 се умножава дружно n – 1 пъти “, продължава той. „ Ако n е 23, отговорът е 0,94. “
Вероятността 0,94 никой да не показа вашия рожден ден е равна на вероятността 0,06 някой да показа вашия рожден ден – а това, признава Хенд, е „ доста малко “. Но ето какво: „ тази възможност не е това, което се пита във въпроса. “
Виждате, че като стартирате със себе си, разглеждате единствено дребна част от вероятните двойки в групата. Да, правилно е, че всеки обособен човек има 364/365 шанса да има рожден ден, друг от вашия – само че въведете втори човек и картината към този момент става по-специална, в сравнение с интуицията ви може да поеме.
„ Вероятността двамата индивида да са с разнообразни дати и третият да няма същия рожден ден като някой от тях е 364/365 × 363/365 “, изяснява Хенд. „ По същия метод вероятността тези трима да имат разнообразни рождени дни и четвърти да не споделя еднакъв рожден ден с някой от тях е 364/365 × 363/365 × 362/365. “
Ако увеличите това пресмятане до 23 души, ще получите възможност нито един от двама души да не споделя един и същи рожден ден от 0,49, което прави вероятността най-малко една двойка да има подобен рожден ден 0,51, или малко повече от половината.
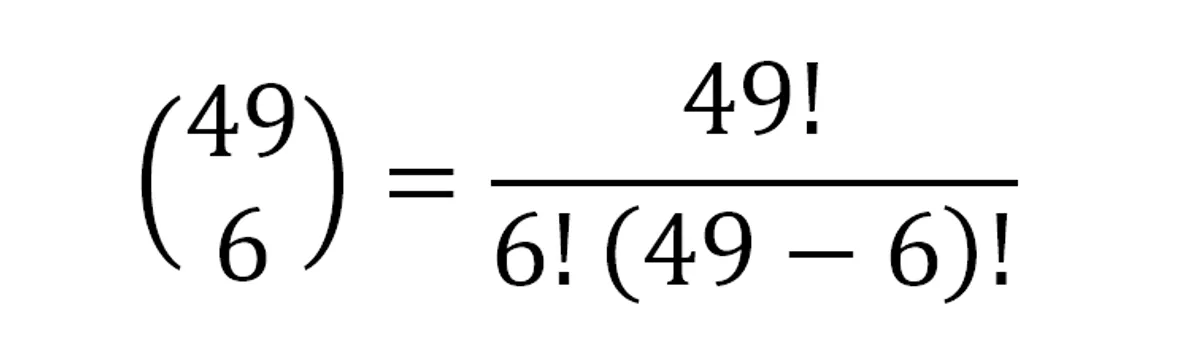
И по този начин, откакто към този момент сме наясно от кое място идват тези по-ниски от предстоящите шансове, по какъв начин да си разбираем идентичните тегления на тотото?
Първо, дано да разгледаме обстановката: Тегленето е 6 от 49, а чиновниците на лотарията по това време декларират, че манипулирането на машините е невъзможно; тегленето „ се организира в наличието на специфична комисия и се излъчва онлайн по националната телевизия, което подсигурява, че няма машинация “, декларират те тогава пред Ройтерс.
Това значи, че всеки набор от 6 цифри се среща 1: 13 983 816 – резултат от уравнението нагоре.
Така че, да, поради избора на 6 цифри през септември – запомнете: 4, 15, 23, 24, 35 и 42 – вероятността тъкмо тази композиция да се повтори е, меко казано, извънредно дребна. Но както и при парадокса на рождения ден, не това е въпросът, който би трябвало да си задаваме.
„ Шансът да съвпаднат е 1: 13 983 816″, съгласи се Хенд. „ Но какво да кажем за шанса две от три тегления да съвпаднат? Или пък шансът да съвпаднат две тегления от 50? “
В края на краищата, изяснява той, във всеки три тегления на лотарията има три евентуални метода две от тях да съвпаднат. При четири тегления има шест вероятни двойки, а при пет тегления – 10. Когато стигнете до 50 тегления, има 1225 вероятни двойки – а при 1000 тегления има 499 500 вероятни метода два набора цифри да съвпаднат.
Това доста покачва възможностите. Докато извършите 4 404 тегления, в действителност е по-вероятно два тиража да съвпаднат тъкмо – и както отбелязва Ханд, „ в случай че всяка седмица се случват по два тиража, което прави 104 за година, това ще отнеме по-малко от 43 години “.
Така видяно, „ Когато вземем поради броя на лотариите по света, виждаме, че би било необикновено, в случай че тегленията не се повтарят понякога “, отбелязва Хенд.
Разбира се, четири дни са надалеч от 43 години – само че е ясно, че дублирането в никакъв случай не е било толкоз извънредно, колкото изглеждаше на пръв взор. Всъщност, в случай че не друго, в последна сметка това е било изключително нещастно събитие: „ Никой не завоюва огромната премия в първото изтегляне “, оповестява BBC по това време.
„ Но рекордните 18 души познават всичките шест цифри в тегленето на 10 септември. “






