Откриха повече от 1000 решения на задачата за трите тела
С помощта на нови изчислителни способи учените са съумели да открият стотици пъти повече фамилии затворени орбити, в сравнение с бяха известни преди този момент, на познатата още от времето на Нютон задача на трите тела, заяви phys.org.
Всички решения са открити за двумерния случай с нулев начален ъглов миг, което още веднъж показва сложността даже при лимитирана дефиниция на задачата.
Екипът китайски математици показа резултатите си в две публикации, едната оповестена в списание Science China-Physics Mechanics Astronomy, а втората - на сървъра за предпечат arXiv.org.
Същността на задачата на трите тела е да се открие по какъв начин три тела ще се движат едно по отношение на друго, взаимодействайки си съгласно закона за гравитацията на Нютон, който я формулира още през 1687 година в " Математически правила на естествената философия ". В случая на две тела, общо решение е добре известно - то е намерено от Йохан Кеплер. Но задачата за три тела се оказа доста по-трудна. С нея са се занимавали доста велики математици и физици като Лагранж, Ойлер, Хамилтън, Поанкаре, Вайерщрас и други
Задачата за трите тела разказва придвижването на частиците под въздействието на два центъра, които притеглят частицата с централни сили, които понижават с увеличение на дистанцията с квадрата на дистанцията. Примери за приложението на тази задача е планета, движеща се в гравитационното поле на две звезди или електрон в електрическото поле на две ядра.
Първите три решения са открити от Леонард Ойлер през 1767 година, когато всичките три тела са на една права. През 1887 година математикът Анри Поанкаре демонстрира, че не съществува общо аналитично решение за задачата с три тела с алгебрични изрази и интеграли.
Изследванията върху казуса доведоха до откриването на така наречен сензитивна взаимозависимост от началните условия (sensitivity dependence of initial condition - SDIC) в безредни динамични системи. Днес на безредната динамичност се гледа като на третата велика научна гражданска война във физиката през 20-ти век, сравнима с теорията на относителността и квантовата механика. По този метод проучванията върху задачата за трите тела има доста значимо научно значение.
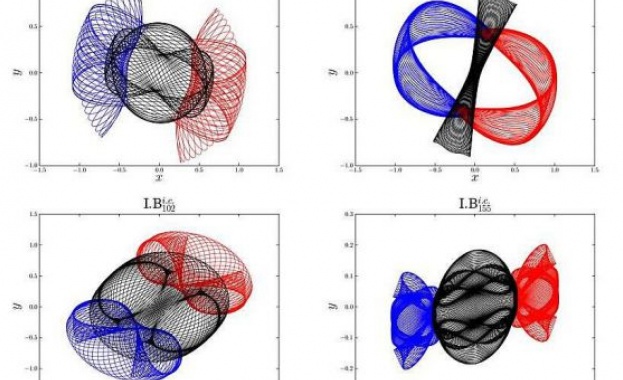
През 1890 година Поанкаре откри, че траекториите на системи с три тела постоянно са непериодични, т.е. да не се повтарят. Това може да изясни за какво е толкоз мъчно да се получат периодически орбити на системи с три тела. За над 300 години проучвания са открити единствено три фамилии периодически орбити. През 2013 година Милован Шуваков (Milovan Šuvakov) и Велко Дмитрашинович (Veljko Dmitrašinović) от Института по физика в Белград вършат пробив, откривайки 13 нови разнообразни периодически орбити, които принадлежат на 11 нови фамилии от Нютоновата задача с три тела с идентична маса и нулев ъглов подтик в тази ситуация на низина [Phys. Rev. Lett. 110, 114301 (2013)].
В първата от двете нови работи на китайските учени Ксиаонинг Ли (XiaoMing Li) и Шидзи Ляо (ShiJun Liao) от Шанхайския университет Джао Тонг, Китай, сполучливо са определили 695 фамилии периодически орбити на една и съща Нютоновата равнинна система с три тела благодарение на суперкомпютъра TH-2 в Гуанджоу, Китай. Математиците употребяват нов способ, наименуван чиста цифрова симулация (clean numerical simulation - CNS), който може да понижи грешките.
Във втората работа е прегледана задачата за три тела с разнообразни маси. В резултат на това са открити 1349 фамилии орбити, от които 1223 са нови.
Математиците означават хубостта и елегантността на графичното показване на новите орбити: " Ние сме изумени и очаровани от тяхното величие ". Те също по този начин показват, че напредъкът се дължи основно на развиването на числените способи, на нови тактики за моделиране на безредните динамични системи и потреблението на суперкомпютри.

Всички решения са открити за двумерния случай с нулев начален ъглов миг, което още веднъж показва сложността даже при лимитирана дефиниция на задачата.
Екипът китайски математици показа резултатите си в две публикации, едната оповестена в списание Science China-Physics Mechanics Astronomy, а втората - на сървъра за предпечат arXiv.org.
Същността на задачата на трите тела е да се открие по какъв начин три тела ще се движат едно по отношение на друго, взаимодействайки си съгласно закона за гравитацията на Нютон, който я формулира още през 1687 година в " Математически правила на естествената философия ". В случая на две тела, общо решение е добре известно - то е намерено от Йохан Кеплер. Но задачата за три тела се оказа доста по-трудна. С нея са се занимавали доста велики математици и физици като Лагранж, Ойлер, Хамилтън, Поанкаре, Вайерщрас и други
Задачата за трите тела разказва придвижването на частиците под въздействието на два центъра, които притеглят частицата с централни сили, които понижават с увеличение на дистанцията с квадрата на дистанцията. Примери за приложението на тази задача е планета, движеща се в гравитационното поле на две звезди или електрон в електрическото поле на две ядра.
Първите три решения са открити от Леонард Ойлер през 1767 година, когато всичките три тела са на една права. През 1887 година математикът Анри Поанкаре демонстрира, че не съществува общо аналитично решение за задачата с три тела с алгебрични изрази и интеграли.
Изследванията върху казуса доведоха до откриването на така наречен сензитивна взаимозависимост от началните условия (sensitivity dependence of initial condition - SDIC) в безредни динамични системи. Днес на безредната динамичност се гледа като на третата велика научна гражданска война във физиката през 20-ти век, сравнима с теорията на относителността и квантовата механика. По този метод проучванията върху задачата за трите тела има доста значимо научно значение.
През 1890 година Поанкаре откри, че траекториите на системи с три тела постоянно са непериодични, т.е. да не се повтарят. Това може да изясни за какво е толкоз мъчно да се получат периодически орбити на системи с три тела. За над 300 години проучвания са открити единствено три фамилии периодически орбити. През 2013 година Милован Шуваков (Milovan Šuvakov) и Велко Дмитрашинович (Veljko Dmitrašinović) от Института по физика в Белград вършат пробив, откривайки 13 нови разнообразни периодически орбити, които принадлежат на 11 нови фамилии от Нютоновата задача с три тела с идентична маса и нулев ъглов подтик в тази ситуация на низина [Phys. Rev. Lett. 110, 114301 (2013)].
В първата от двете нови работи на китайските учени Ксиаонинг Ли (XiaoMing Li) и Шидзи Ляо (ShiJun Liao) от Шанхайския университет Джао Тонг, Китай, сполучливо са определили 695 фамилии периодически орбити на една и съща Нютоновата равнинна система с три тела благодарение на суперкомпютъра TH-2 в Гуанджоу, Китай. Математиците употребяват нов способ, наименуван чиста цифрова симулация (clean numerical simulation - CNS), който може да понижи грешките.
Във втората работа е прегледана задачата за три тела с разнообразни маси. В резултат на това са открити 1349 фамилии орбити, от които 1223 са нови.
Математиците означават хубостта и елегантността на графичното показване на новите орбити: " Ние сме изумени и очаровани от тяхното величие ". Те също по този начин показват, че напредъкът се дължи основно на развиването на числените способи, на нови тактики за моделиране на безредните динамични системи и потреблението на суперкомпютри.

Източник: cross.bg

КОМЕНТАРИ